Aggressive Cows - SPOJ

Being the most upvoted problem on SPOJ, Aggressive Cows forces you to think like an Algorithmist. I have seen a lot of people (including me) who are getting started with competitive programming, struggle with this problem.

But once you get the gist of how to approach it, the implementation part becomes fairly straightforward.

The problem description can be read here.

Overview: All the C cows must be placed in the N stalls such that the minimum distance between any two of them is as large as possible. Print the largest distance.

Solution: Lets first define a function chk(x) that checks if a distance x is possible between each of the cows. We can use a greedy approach here by placing cows at the leftmost possible stalls such that they are at least x distance away from the last-placed cow.

// check if a distance of x is possible b/w each cow
bool chk(int x)
{
  // greedy approach, put each cow in the first place you can
  int cows_placed = 1, last_pos = A[0];
  for (int i = 1; i < N; i++)
  {
    if ((A[i] - last_pos) >= x)
    {
      if (++cows_placed == C)
        return true;
      last_pos = A[i];
    }
  }
  return false;
}

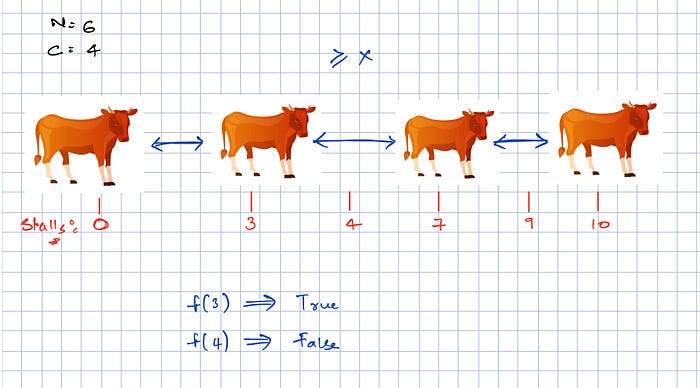
As you can see in the above picture, we have taken the stall locations in increasing order. Therefore, we need to sort our array A that stores stall locations.

Once we have our sorted array, we can apply the Binary Search algorithm on the sorted input, and use our function chk(x) to find the largest distance possible.

#include <iostream>
#include <algorithm>
using namespace std;
int N, C;
long long A[100000];

void solve()
{
  cin >> N >> C;
  for (int i = 0; i < N; i++)
    cin >> A[i];
  sort(A, A + N);

  // binary search 
  long long low = 0, high = 1000000000, mid, pos = 0;
  while (high >= low)
  {
    mid = (high + low) / 2;
    if (chk(mid))
    {
      low = mid + 1;
      pos = mid;
    }
    else
    {
      high = mid - 1;
    }
  }
  cout << pos << endl;
}

int main()
{
  int T;
  cin >> T;
  while (T--)
    solve();
  return 0;
}

Time Complexity: O(NlogN), Space Complexity: O(N); Where N ≤ 100000.